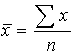Measures of central tendency
Characteristics of Distributions
Central Tendency (or Location)
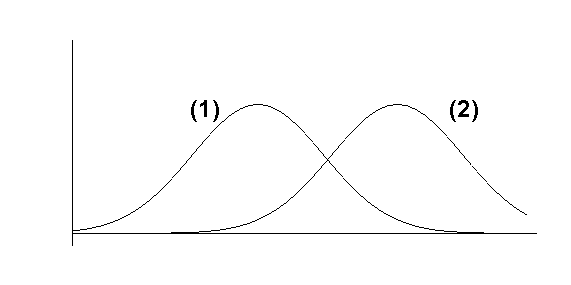
Arithmetic Mean
This is the most useful
of the three measures of location. If ![]() are
are ![]() observations on a variable X then the arithmetic mean
observations on a variable X then the arithmetic mean ![]() , is defined as:
, is defined as:
![]()
If the observations are grouped, ie
i.e.
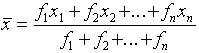
This situation arises in two cases:
i.e.
(i) when the classes are individual discrete values as in the radiation data:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The easiest way to perform the calculation is to use the statistical facilities of a scientific calculator. Find the "mean" button on your calculator, usually marked
(i) The thickness of the magnetic coating was measured at 10 randomly
chosen points on the surface of a flexible disc produced by a manufacturer. The
following results, in microns ![]() were obtained.
were obtained.
Thickness 973 975 976 977 976 980 981 977 979 976
The mean thickness is given by ![]() 977 microns
977 microns
(ii) We have already met the following data on the heights of trees
| Height (cms) | Frequency (f) | Class midpoint |
|
| ||
| 49.5 - 79.5 |
|
64.5 |
| 79.5 - 109.5 |
|
94.5 |
| 109.5 - 139.5 |
|
124.5 |
| 139.5 - 169.5 |
|
154.5 |
| 169.5 - 199.5 |
|
184.5 |
| 199.5 - 229.5 |
|
214.5 |
| 229.5 - 259.5 |
|
244.5 |
|
|
In this case
The Median
(a) Discrete Distribution
Consider a
set of data on a discrete variable. Arrange the data in ascending or descending
order of magnitude then the median is: (i) the middle item for an odd number of
observations, (ii) the average of the two middle items for an even number of
observations. In general if there are n observations the median is the
value of ![]() th observation .
th observation .
For example:
2, 5, 6, 8, 13, 15, 19, 22, 38 have median 13(b) Continuous Distributions
3, 4, 8, 9, 13, 16, 17, 20, 21, 22 have mediani.e. 14.5
The median divides the area under the frequency distribution diagram (ie the histogram) into two equal parts. Whilst there is a special formula for calculating the median for a grouped frequency distribution it is probably easiest to estimate it from the ogive by drawing a line across at the 50% level on the % cumulative frequency (vertical) scale to the curve and then down to the horizontal scale to read off the estimate (see the picture above of the ogive).
The main difference between the median and the mean is that the median is insensitive to extreme values since, unlike the arithmetic mean, it does not take into account the actual value of each observation, but only considers the rank of each measurement.
The median is useful in such areas as lifetime testing of components.
Quartiles
The upper and lower quartiles
(together with the median) divide the observations into quarters. For
n observations on a discrete variable the upper and lower quartiles are
the values of the ![]() and the
and the ![]() observations respectively when they are arranged in ascending order of
magnitude.
observations respectively when they are arranged in ascending order of
magnitude.
For a distribution on a continuous variable the quartiles are, like the median, easy to estimate from the ogive by drawing lines across at 25% and 75% on the vertival scale and then down to the horizontal scale and reading them off (again see the picture above of the ogive).
The Mode
The MODE of a set of
observations is the value that occurs most frequently. When designating
the mode for a grouped frequency distribution, we usually refer to the MODAL
CLASS, where the modal class is the class with the highest frequency. If a
single value for the mode of grouped data must be specified, it is taken as the
midpoint of the modal class.
For example, for the data on the height of nine year old trees, the modal class is 169.5 -199.5(cm) so that 184.5 cm would be taken as the mode.
The disadvantage with the mode as a measure of location is that it is not always unique, ie a distribution can have more than one mode.
For grouped data the mode is not uniquely defined, since changing the class intervals may give different maximum frequencies.
Dispersion (Spread or Scatter)
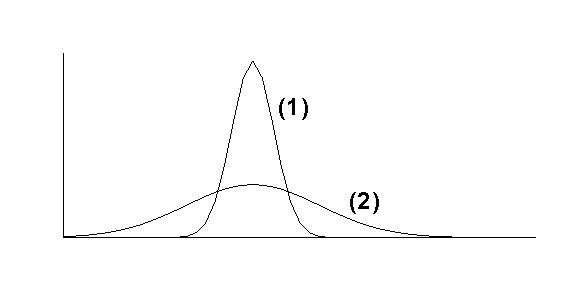
The Range
The RANGE of a set of observations is the difference
between the greatest and least of the observations. It is easy to calculate and
is widely used in industrial quality control as one check on manufactured items.
However, it ignores the distribution of the observations between the extremes
(eg possible concentrations about the centre) and is too easily affected by
freak results.
For example: 2.3 4.1 5.2 6.9 8.8 9.4 have range = 9.4 - 2.3 = 7.1.Semi-Interquartile Range
Also 2.3 6.1 6.2 6.4 6.6 9.4 still have range 7.1
This is defined as: siqr = ½ (upper quartile - lower quartile)
Again this is fairly easy to calculate, is not so easily affected by freak results and is useful for comparing the dispersion of similarly shaped distributions.