Plotting and displaying data

Summarising and Grouping Data
A large set of statistical data conveys very little information as it stands and it is usually helpful to summarise it in a more concise form before attempting to draw any conclusions.  Observed data can be divided into classes by grouping together those observations having a particular characteristic in common.

The number of observations falling into a particular class, or cell, is called the FREQUENCY, f, corresponding to that class.  The complete set of observations can be summarised by the frequencies corresponding to each class. This is termed a FREQUENCY DISTRIBUTION.

Notation
The variable observed is denoted by a capital letter, eg X, and the values that X can have are denoted by the corresponding small letter .

(a) Discrete Variables
Consider the data on the number of particles emitted by a radio-active source.  Here X is the number of particles emitted and  etc represent the observed values.

We can construct the frequency table as follows:


The above method of forming a frequency distribution is somewhat antiquated. The procedure is much more efficient if you use a spreadsheet program like Excel.
A frequency distribution for a discrete variable can be presented graphically by means of a bar chart  This consists of a set of rectangles, the heights of which represent the frequencies. However, in most practical examples the width of each rectangle is made the same so that the area is also proportional to the frequency. We shall see that in certain circumstances it is more convenient to represent frequencies as areas.

Consider the frequency distribution on the number of particles emitted by a radio-active source.

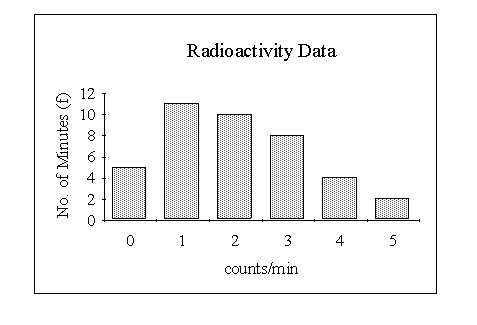
By a simple change of scale the bar chart can be drawn so that it represents the relative frequency (or percentage of the total). This makes comparison of two or more bar charts easier.

Grouping of data
Consider now the data showing the number of radio-active particles emitted in 10 minute periods. With such a wide range of possible numbers of particles (the smallest number is 5 and the largest 39) it is obvious that, with the limited amount of data available, simply finding the frequencies corresponding to each value of X would result in many zero scores. In order to obtain some idea of the distribution it will be necessary to group the data by finding the frequencies corresponding to classes of values of .  For example

 
Note that each class is denoted by two values. These are termed the lower and upper class end marks.  We may define a class midpoint for each class as the mean of respective class end marks. In the above example the class midpoints are 7, 12, 17, 22, 27, 32, 37. Class midpoints are useful reference points when drawing bar charts.

We define the class interval, c, as the difference between one class midpoint and the next higher one. In the above example the class interval is 5.  Finally, for each class we define a lower and upper class boundary as follows:

                    lower class boundary = class midpoint 

                    upper class boundary = class midpoint 

For the above example the classes may be described by means of the class boundaries:
 

class
4.5 - 9.5
9.5 - 14.5
14.5 - 19.5
19.5 - 24.5
24.5 - 29.5
29.5 - 34.5
34.5 - 39.5
 
The bar chart for the data uses the class end marks to identify each class, as shown below.
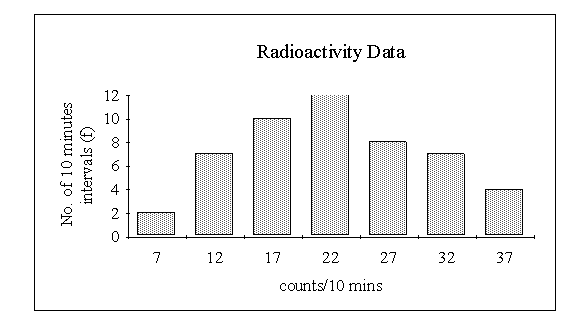
The choice of classes is largely a matter of judgement and will depend upon the number and range of observations. The number of classes should normally lie between 6 and 15.

(b) Continuous Variables
If measurements are quoted with a given specified accuracy the exact class boundaries can be determined.  For example a table showing the distribution of plant heights might be

            height (to nearest cm)     60 - 62     63 - 65     66 - 68     etc

            frequency                             6             18             14

In this case the classes are really, 59.5 to 62.5, 62.5 to 65.5, 65.5 to 68.5, etc.

A frequency distribution for a continuous variable is presented graphically by means of a HISTOGRAM (this is the name given to a bar chart based on continuous data). Note that adjacent bars in a histogram are drawn touching each other, whereas in the other bar charts discussed they generally are not.  Consider the following example:

The heights (in cm) of 140 nine year old trees of a certain type were measured. The following table shows the data grouped into classes:
 

height (cms) frequency
50 - 79 7
80 - 109 11
110 - 139 14
140 - 169 21
170 - 199 42
200 - 229 35
230 - 259 10
 
In this case the classes are really 49.5 - 79.5, 79.5 - 109.5, etc.
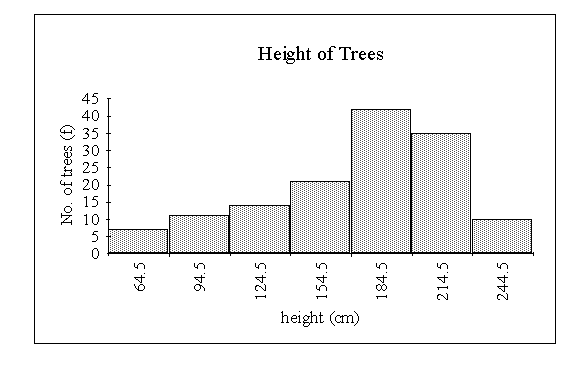
Note that, as before, the area under any part of a histogram corresponds to the number (or proportion) of observations which fall into any specific interval.

Frequency Polygon
Often a FREQUENCY POLYGON is drawn rather than a histogram. This is done by plotting the frequency of each class as a dot at the class midpoint and then connecting each adjacent pair of dots by a straight line. This is, of course, the same as if the midpoints of the tops of the rectangles of the histogram are joined by straight lines. Frequency polygons are also commonly used for discrete distributions. The frequency polygon for the distribution of tree heights is:

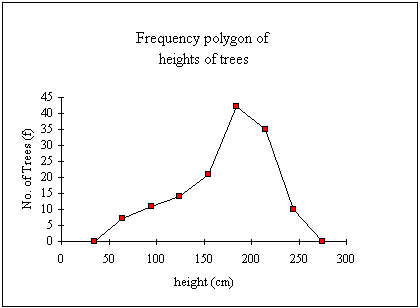
Notice that the polygon is extended down to the horizontal axis to the mid-points of the classes that could be added at either end of the distribution, ie 34.5 and 274.5.

Frequency polygons are arguably more useful in the visual comparison of two or more frequency distributions than histograms.

 

from SHU Science & Maths, 1998